Le modèle normal est une loi de probabilité découverte indépendamment par les mathématiciens Gauss en Allemagne en 1809 et Laplace en France en 1812.
La loi de Laplace et Gauss est importante en pratique car elle permet de représenter la variabilité de nombreux phénomènes naturels. C’est elle, aussi, qui modélise les variations observées entre mesures successives d’une quantité.
Le théorème central limite explique pourquoi on rencontre si fréquemment dans la nature des lois normales faisant d’elles une clé nécessaire à la démarche statistique.
Le modèle normal centré réduit
Il existe un nombre important de lois normales. Nous nous intéressons ici plus précisément au théorème de Moivre-Laplace, autrement appelé modèle normal centré réduit qui permet, de manière simplifiée, de déterminer la probabilité d’obtenir une valeur par rapport à deux valeurs centrales de la population concernée : la moyenne et l’écart type :
- « Centré » parce que l’on va utiliser la représentation du modèle normal en plaçant la moyenne au centre, comme si elle était égale à 0.
- « Réduit » parce que l’on va analyser la distance entre la moyenne et la valeur étudiée en nombre d’écart-type.
Le théorème de Moivre-Laplace peut s’utiliser pour des phénomènes :
- continus : âge, taille, …
- à causes multiples (modification d’états simultanément) : pièce de monnaie dont la masse dépend du volume et de la densité de matière utilisée
- à causes additives
Le modèle normal centré réduit peut s’utiliser pour évaluer, par exemple, le pourcentage de chances de réaliser un chiffre d’affaires maximum sur les ventes d’un produit ou encore estimer la durée de vie d’un produit.
Moivre mesure l’écart entre la valeur étudiée et la moyenne selon la formule suivante pour t la variable réduite :
Il utilise ensuite la variable réduite pour lire la probabilité correspondante dans la table de la loi normale établie sur la base des travaux de Christian KRAMP qui a calculé l’augmentation d’aire pour toutes les valeurs de x dans le cadre de ses travaux sur les factorielles et plus particulièrement la fonction gamma.
Représentation graphique
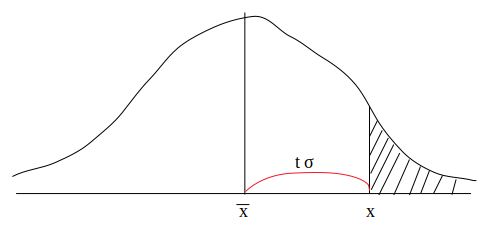
Comme pour tout modèle normal :
- 65% de la population est comprise entre la moyenne et +/- 1 écart-type
- 90% de la population est comprise entre la moyenne et +/- 2 écarts-types
- 99% de la population est comprise entre la moyenne et +/- 3 écarts-types
Table de probabilité
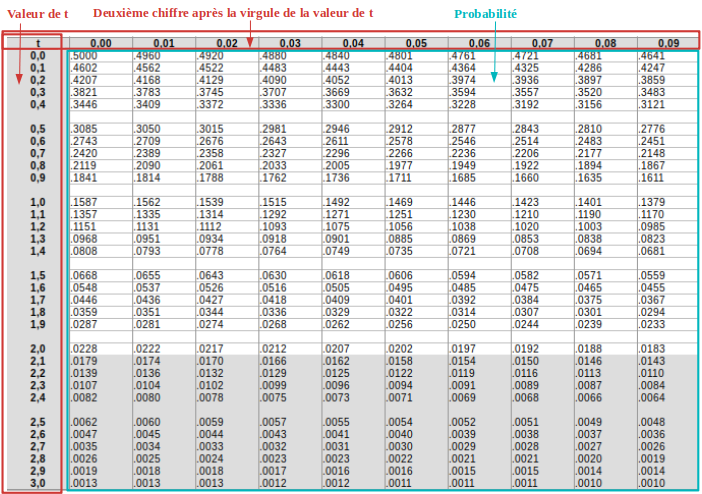
Cette table permet de lire la probabilité correspondant à la valeur de la variable réduite t calculée pour une valeur x donnée :
Attention ! Les valeurs des probabilités sont applicables lorsque t>0 et que l’on cherche la probabilité de trouver des individus supérieurs à x. C’est ce qu’explique la représentation graphique ci-dessus. Les valeurs sont également applicables si t<0 et que l’on cherche la probabilité de trouver des individus inférieurs à x.
Ainsi, si t>0 et que l’on cherche la probabilité de trouver des individus inférieurs à x, il convient d’effectuer le calcul « 1-probabilité de la table ».
Il en va de même si t<0 et que l’on cherche les individus supérieurs à x.
Mémo et table normale :
Exemples d’application
Lecture des probabilités
Considérons une population dont la moyenne est de 60 et l’écart-type de 2.
Probabilité qu’un individu (x) ait une valeur supérieure à 61
Calculons la valeur de t :
t= (61-60) / 2 = 0,50
En se basant sur les valeurs de la table, pour t=0,5 on trouve « .3085 », c’est à dire 30,85 %, soit environ 31 % de probabilité qu’un individu ait une valeur supérieure à 61.
Probabilité qu’un individu (x) ait une valeur supérieure à 57
Calculons la valeur de t :
t= (57-60) / 2 = -1,50
En se basant sur les valeurs de la table, pour t=1,5 on trouve « .0668 », c’est à dire 6,68 %, soit environ 7 %.
Comme t<0 et que l’on cherche la probabilité qu’un individu soit supérieur à 57, on effectue le calcul de probabilité comme suit :
P = 100 – 7 = 93 %
Il y a donc 93 % de probabilité de trouver une valeur supérieure à 57.
Probabilité qu’un individu (x) ait une valeur entre 57 et 61
D’après les 2 exemples précédents, nous cherchons la probabilité lorsque t est compris entre -1,5 et +0,5.
Sachant que la probabilité qu’un individu ait une valeur > 61 est de 31 % avec t = 0,5, on peut en déduire que la probabilité qu’un individu ait une valeur < 61 est de 100-31 soit 69 %.
Nous savons également que la probabilité pour t = 1,5 est de 7 % ce qui signifie que que la probabilité qu’un individu ait aune valeur inférieure à 57 (moyenne – 1,5 écart type ou t=-1,5) est de 7%.
Nous pouvons donc en conclure que la probabilité qu’un individu ait une valeur comprise entre 57 et 61 et de 69-7 = 62 %.
Nous pouvons mener le raisonnement similaire en sachant que 93 % des individus ont une valeur supérieure à 57 et que 31 % ont une valeur supérieure à 61. Ce qui nous donne le calcul de probabilité P = 93-31 = 62 %.
Nous pouvons aussi dire que 7 % des individus ont une valeur inférieure à 57 et que 31 % des individus ont une valeur supérieure à 61. Ce qui nous donne le calcul de probabilité P = 100 – (7+31) = 62 %.
Probabilité qu’un individu (x) ait une valeur entre 61 et 63
Nous cherchons la probabilité lorsque t est compris entre +0,5 et +1,5 ((63-60)/2).
Nous savons que la probabilité de trouver des valeurs supérieures à 61 est de 31 % et que la probabilité de trouver des valeurs supérieures à 63 (t=1,5) est de 7 %.
Nous pouvons donc en déduire le calcul de probabilité P = 31-7 = 24 %.
Nous pouvons aussi considérer que la probabilité de trouver des valeurs inférieures à 61 est de P = 100 – 31 = 69 %.
Dans ce cas la probabilité de trouver des valeurs comprises en 61 et 63 est de P = 100 – (69 + 7) = 24 %.
Dans le multi-bornage (part d’individus compris entre deux valeurs), préférer le calcul sur les extérieurs en excluant les valeurs hors bornage. Utiliser les décimales pour les calculs mais arrondir le résultat.
Pour aller plus loin, je vous recommande cette publication : https://commentprogresser.com/statistique-distribution-loi-normale.html